Digitally enhanced boardgame - Part 3: Perspective

Link to Part 2

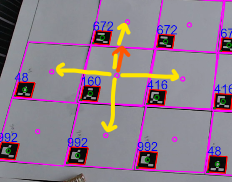
Since the camera is not perfectly looking at the game from a top-down perspective and other things like camera-distortion come into play, the corner coordinates of a marker do not form a perfect square.
If you have a fixed playing field the easiest approach would be to put a marker in each corner and translate between distorted camera-coordinates to top-down coordinates. In this example I'm using the js library perspective-transform

The square piece of paper could be the playing field or it could be used as a one-time camera calibration pattern, provided that the camera is not moved after that.
This works pretty reliably but I did not end up using it because of two main concerns regarding the dungeon tiles:
- the playing field is limited by the size of the piece of paper
- the playing field determines the dungeon grid, not the tiles
- if each tile has a marker on it, the corner-markers become redundant
In my second approach I took the corner coordinates of each marker and projected the edges outward using the information that the markers have a specific size in the real world (200mm) and the tiles have a specific size (600mm).
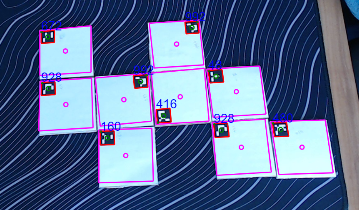
The result looks something like this:

The tile corners do not match up perfectly but its close enough!
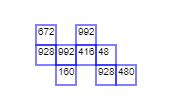
To the human eye it already looks like a grid but for the computer its just an array of random points.
So how do we map this to a grid? I researched for a bit but the only thing that kind of made sense to me was "Fitting an orthogonal grid to noisy points" which needs complicated stuff like Hough transform and k-means.
So I decided to give it a try and implement something myself. My algorithm starts from the start-tile and discovers the rest of the dungeon step by step through looking at neighboring tiles, here is the pseudo-code:
1) define an "open list" and a "closed list"
2) put the start tile in the openlist
3) while there are items in the openlist
3.1) take an item out of the openlist
3.2) put tile into closedlist
3.3) calculate "up-vector" from the tile center to the center of the top edge
3.4) find all tiles that are not in the openlist or closedlist and where the distance between its center and the current tile's center is within a certain threshold
3.5) for each of these direct neighbours
3.5.1) calculate the angle between the center to center vector and the up-vector of the tile, this gives us the relative position of the neighbour (something like (-1,0) for "up")
3.5.2) save the neighbour to the final grid at current tile pos + relative position
3.5.3) add the neighbour to the open list