Wave Function Collapse Experiment

So right from the start: apparently it has nothing to do with the quantum concept it was named after ^^

There seem to be two versions: texture and tile mode. I will be using tile mode.

For a better explanation check out this awesome article by Boris!

Tiles and Edges

In my code, a tile has an image and 4 edges. An edge of a tile is expressed as a String, for example "010" or "ABA". Two tiles can be placed next to each other if the touching edges match.

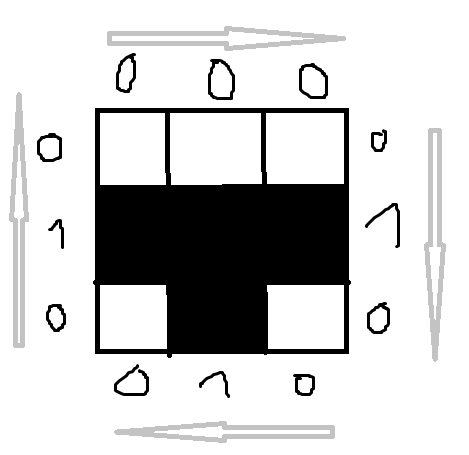
The "T" example is especially easy because all edges are symmetrical. If not you have to mirror one edge when comparing them.

For example if the left edge of tile A is "100" and the right edge of tile B is "001", the comparison is:

B right    A left
0          0
0          0
1          1

As you can see the edges match, because left is read from bottom to top and right is read from top to bottom. Imagine rotating the tile so that the edge you are inspecting is at the top and you read from left to right. Alright, enough confusion.

First implementation

The first basic implementation went like this:

• have a grid
• each cell has a stack of its possible choices (initially its an array of all tiles)
• repeat until every cell is collapsed:
  • find the cell with the least amount of choices
  • take one of the choices and set it as the cell's tile, the cell is now "collapsed"
  • update the neighboring cells so that they only keep the choices that still "work" (the choices where the edges towards all collapsed neighboring tiles match)

To start things of I tried a simple "T" tile, a 3x3 tile and all its rotations

import Tile from "../Tile.js";

let tiles = [];
let t = new Tile("t.png", [
    "000",  //top
    "010",  //right (top to bottm)
    "010",  //bottom
    "010"   //left (bottom to top)
]);
tiles.push(t);
tiles.push(t.rotate(1));
tiles.push(t.rotate(2));
tiles.push(t.rotate(3));

export default tiles;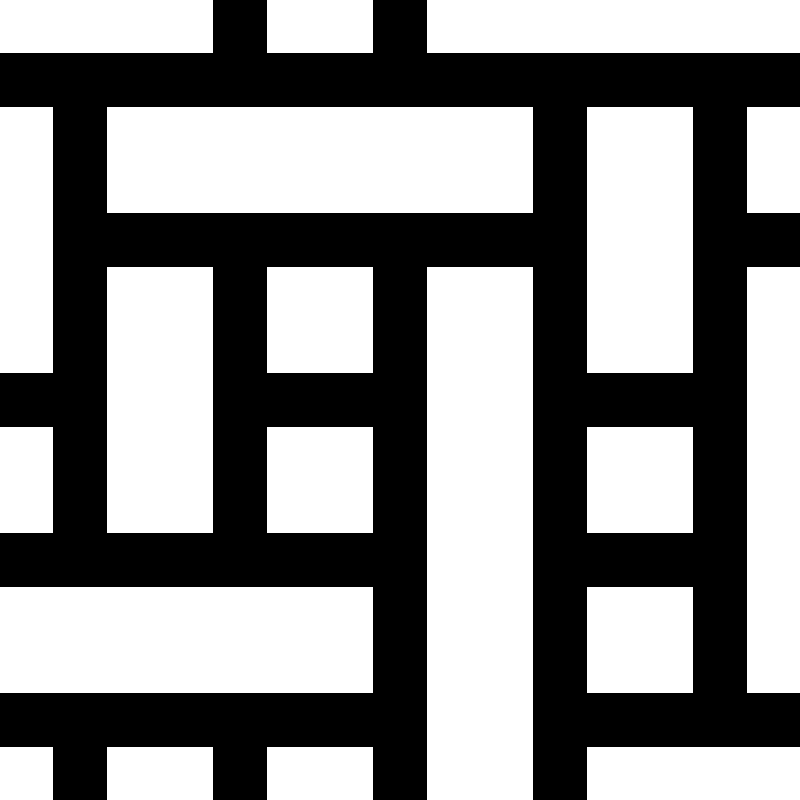

Looks great! But our simple "T" example has one more convenient feature: It always results in a full grid. The algorithm will always find a fitting tile choice.

If you only had the "T" tile and not all of its rotations, the algorithm does not know what to do:

In the example above it is not possible to make a full grid at all. Now let's imagine we have a tileset that allows a full grid but has somehow generated into a situation where a cell has no available choices, what do we do?

Backtracking

• if the cell the algorithm has chosen to collapse has more than 1 choice, we have to make a random choice, a "guess"
• create a "savepoint"
  • a copy of the grid
  • the cell we are collapsing
  • the choice we made
• push the savepoint to a stack

now if we reach a point where a cell has no choices, we take the last savepoint from the stack

• restore the grid to the one in the savepoint
• remove the choice we took from the cell of the savepoint, because apparently it will lead to a messed up grid
• try again

New tileset, new problems

After the "T" example I chose a more complex set of tiles where each edge has 5 characters. As you can see in the image below, this does generate a full grid, but because a "000" edge matches a "000" edge, and most tiles have at least one of these "empty" edges, it leads to several "islands" of connected rooms:

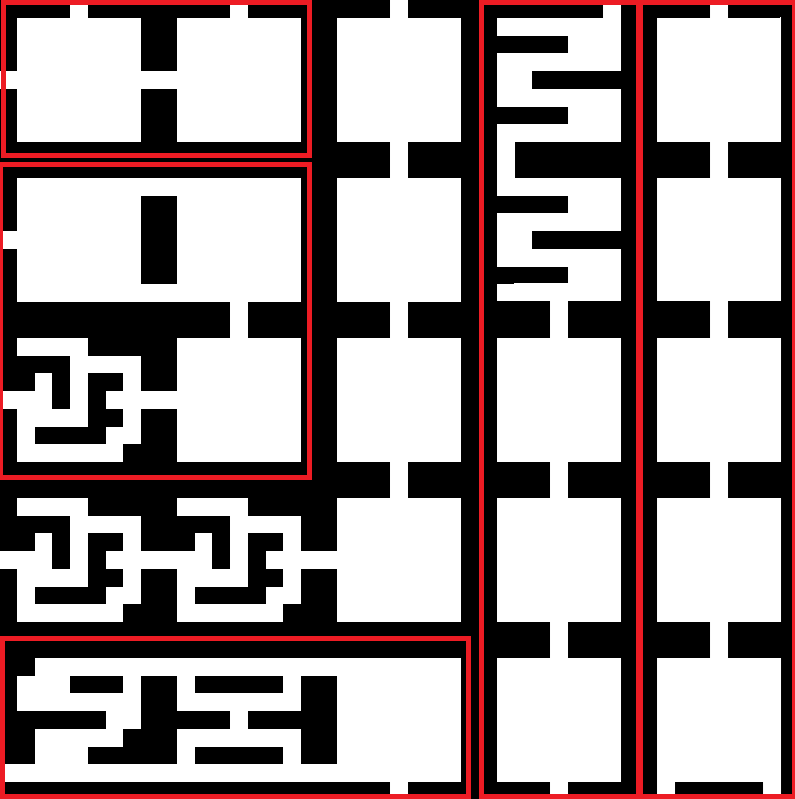
My solution to this is to modify the way the algorithm chooses a cell to collapse:

let connectableCells = cells.filter(cell => {
            let neighbours = grid.directNeighbours(cell.x, cell.y);
            let connectedChoices = cell.choices.filter(choice => {
                let tile = tiles[choice];

                //for each neighbour, check if it exists and is collapsed
                //if it is, check if the edge towards this neighbour is not empty
                //then check if we do connect to that neighbour

                if (neighbours.n && neighbours.n.collapsed && !isEmptyEdge(tile.getTopEdge()) && doEdgesMatch(tiles[neighbours.n.tile].getBottomEdge(), tile.getTopEdge())) return true;
                if (neighbours.s && neighbours.s.collapsed && !isEmptyEdge(tile.getBottomEdge()) && doEdgesMatch(tiles[neighbours.s.tile].getTopEdge(), tile.getBottomEdge())) return true;
                if (neighbours.w && neighbours.w.collapsed && !isEmptyEdge(tile.getLeftEdge()) && doEdgesMatch(tiles[neighbours.w.tile].getRightEdge(), tile.getLeftEdge())) return true;
                if (neighbours.e && neighbours.e.collapsed && !isEmptyEdge(tile.getRightEdge()) && doEdgesMatch(tiles[neighbours.e.tile].getLeftEdge(), tile.getRightEdge())) return true;

                return false;
            });

            return connectedChoices.length > 0;
        });

• check each uncollapsed cell
  • for each choice the cell has
    • look at the top neighbor of the cell
      • if the top neighbor exists
      • and it is collapsed
      • and the top edge of the current choice is not an "000" empty one
      • and the bottom edge of the top neighbor matches the top edge of the current choice
      • then this choice results in a connection
    • repeat for the other neighbors
  • if there is at least one choice that results in a connection to a neighboring cell, the cell is considered as a possible candidate
• only if there are no possible candidates, fall back to the "least entropy" algorithm

One thing I noticed is that in some cases this results in a very, very long run time. It will finish eventually, but it will take considerably longer than usual. It seems like sometimes the initial starting-tile forces the algorithm to backtrack so much that it hardly makes any progress.

My dirty hack is to simply restart the whole generation if the loop is running for more than 1000 iterations 😬

Balance

When designing a tile set my assumption is that you really have to keep a balance of edges.

Example 1: If there is only one tile with the right edge "001" and only one tile with the left edge "100" then these two tiles will always appear together. Because of this, they both become more rare.

Example 2: If a tile is the only tile with a certain edge, it will only occur if that edge faces the boundary of the canvas.

Example 3: If there are more tiles that match each other on the top/bottom edges than there are tiles that do on the left/right edges, the path is more likely to expand vertically than horizontally.